Lab 6 - Sorting

On competing the lab you will:

Implement a comparable class.
Generate random data for testing.
Sort using insertion and Selection sort.
Compare the performance of selection and insertion sort.

Eclipse: Data Generation

Create a new project in Eclipse called Lab6Sorting1.

Data Generation

Create an implementation of the simplified Date class as shown in lecture slides. In addition:
- add getters for all fields in the class.
- Add a suitable toString() method.
Create implementations of both the Selection sort and Insertion sort algorithms as described in the lecture slides. Remember that the less() and exch() methods in both Insertion and Selection are exactly the same, only the sort() method changes.
Create a utility class called DateArrayGenerator that contains a method:
```
public static Date [] randomDateArray(int n)
```
that returns an array of n random dates over the last 100 years(1915-2015). Use the Date class from step 1. You can ignore accounting for leap years if you wish. Test it by including a main method in the class that outputs the following when run: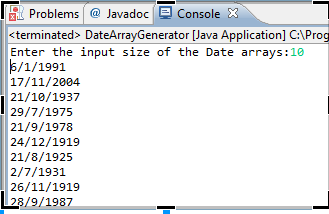

Algorithm Comparison

You know from lectures that the efficiency class of both insertion and selection sort is quadratic for random arrays. Furthermore the running time should increase at a similar rate for larger inputs but insertion should be slightly faster. Prove this using an empirical approach as follows: Using the Insertion and Selection classes from the previous section, develop an executable Java class called SortCompare that contains the following method:

public static double time(String alg, Comparable[] a) {

        double startTime = System.currentTimeMillis();
        if (alg.equals("Insertion"))
            Insertion.sort(a);
        if (alg.equals("Selection"))
            Selection.sort(a);

        return System.currentTimeMillis() - startTime;

    }

Now create another method in SortCompare that calculates the average running time for k random arrays of size n. Refer to the slides for empirical analysis of algorithms for ideas. The signature of the method should be:
```
public static double timeRandomInput(String alg, int n, int k)
```

Finally, write a main method similar to the following that compares the running time of the two algorithms. You can change the size and number of random arrays (1000 and 100 respectively is manageable but remember these are quadratic algorithms!)

public static void main(String[] args) {

            String alg1 = "Insertion";
            String alg2 = "Selection";

            StdOut.println("Enter the input size of the Date arrays:");
            int n = StdIn.readInt();
            StdOut.println("Enter the number of different inputs to be generated:");
            int k = StdIn.readInt();
            double t1 = timeRandomInput(alg1, n, k); // total for alg1
            double t2 = timeRandomInput(alg2, n, k); // total for alg2
            StdOut.printf("For %d random Dates\n %s is", n, alg1);
            StdOut.printf(" %.1f times faster than %s\n", t2 / t1, alg2);


    }

Do a couple of runs on your computer and see if the results match to what you expected from the notes.
As a challenge, try to modify your SortCompare class to generate a partially sorted array instead of random. Then compare the running times again. If the theory is correct, Insertion should be quicker.